Analyses et lois statistiques de répartition
 L’analyse des pluies permet de définir certaines tendances générales de pluviosité. Ces lois statistiques indiquent notamment les relations entre l’intensité (la hauteur de précipitations par unité de temps), la durée (le temps écoulé entre le début et la fin de la précipitation) et la fréquence d’apparition (le nombre d’occurrences) d’un événement pluvieux.
L’analyse des pluies permet de définir certaines tendances générales de pluviosité. Ces lois statistiques indiquent notamment les relations entre l’intensité (la hauteur de précipitations par unité de temps), la durée (le temps écoulé entre le début et la fin de la précipitation) et la fréquence d’apparition (le nombre d’occurrences) d’un événement pluvieux.
Intensité-durée
L’intensité et la durée dépendent largement des processus à l’origine des précipitations (système nuageux, humidité disponible, degré d’instabilité atmosphérique) mais aussi des mécanismes au cours de la chute vers le sol (fonte, évaporation, sublimation). Ainsi, en fonction de ces caractéristiques météorologiques, la durée d’une averse peut varier de quelques minutes à une centaine d’heures pour une superficie allant de quelques kilomètres carrés (orages) à quelques milliers de kilomètres carrés (pluies cycloniques), tout en connaissant plusieurs pointes d’intensité. Les statistiques à l’échelle du globe terrestre suggèrent que l’intensité des précipitations est plus ou moins proportionnelle à l’inverse de la racine carrée de la durée, mais il existe cependant de grandes variations spatiales. Alors qu’aux latitudes tempérées, l’intensité dépasse exceptionnellement 200 mm/h pendant quelques instants lors des orages d’été, sous les tropiques, des précipitations de ISO mm en une heure se produisent régulièrement et des taux de 340 mm/h en quelques minutes ont déjà été enregistrés. Ces précipitations, rares et de nature orageuse, lorsqu’elles se produisent sur un sol sans protection, provoquent rapidement la fermeture de ce sol, et la formation d’un ruissellement, avec un très haut pouvoir érosif à l’origine de dégâts importants (destruction de sols agricoles et de voies de communication).
Hauteur-durée
L’intensité pluviométrique n’est pas directement liée aux totaux pluviométriques d’une période de l’année, qui dépendent plutôt du nombre de jours de pluie. On a mis en évidence, à partir des précipitations extrêmes à l’échelle du globe terrestre, l’existence d’une relation forte entre hauteur et durée des pluies .
Fréquences et courbes ID F
Lafréquence d’apparition de certains événements extrêmes est une donnée essentielle à prendre en compte dans les problèmes d’aménagement et, plus particulièrement, de gestion des risques. La période de retour équivaut à l’intervalle moyen avec lequel un événement donné a une probabilité statistique d’être égalé ou dépassé : un événement qui a une fréquence statistique de 0,01 possède une période de retour de 100 ans. Ainsi, une pluie, caractérisée à la fois par sa durée et sa hauteur, de période de retour T, est la pluie qui sera dépassée au moins une fois toutes les T années : on parlera de pluie décennale ou centennale. Les valeurs critiques de période de retour varient selon les facteurs physiques, notamment météorologiques et topographiques, mais aussi économiques, sociaux et politiques (type d’aménagement territorial, activités agricoles, expansion urbaine, politique de gestion du risque hydroclimatique…).
L’accès à de très longues séries instrumentales est nécessaire pour définir ces probabilités. La période de retour est souvent estimée à partir des courbes intensité- durée-fréquence (IDF).
Ces courbes, qui résument l’essentiel des caractéristiques des pluies, sont fondamentales dans de nombreuses applications hydrologiques, par exemple pour le calcul des réseaux d’évacuation des eaux pluviales pour lequel on a besoin de déterminer une «pluie de projet» prenant en compte la durée et la hauteur de la précipitation, ou encore pour le dimensionne- ment d’un ouvrage de retenue. Les courbes IDF sont le plus souvent établies à partir de lois statistiques qui peuvent conduire à des résultats assez éloignés les uns des autres {cf. encadré). Ces valeurs statistiques sont donc des informations intéressantes, mais elles ne sont en aucun cas des valeurs rigoureuses.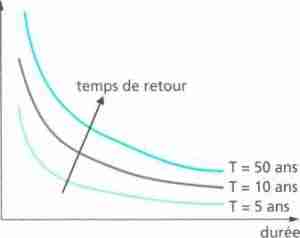
Vidéo : Analyses et lois statistiques de répartition
Vidéo démonstrative pour tout savoir sur : Analyses et lois statistiques de répartition