Les architectes des formes: les tisserands du vivant
Pour expliquer le parallèle entre les organes et les flocons de neige, il faut revenir à la forme du doigt. La peau du doigt, si on enlève l’os et tout ce qui est dans le doigt, ce n’est jamais qu’une peau en forme de tuyau bouché au bout. Ça ressemble à une extrémité de tuyau de poumon, ou de rein en croissance. Or nous avons vu qu on ne peut pas coucher les fibres sur le bout d’un tel tuyau n importe comment : il reste des coutures qui tendent à former des petites éminences, des pointes qui saillent. En ce sens, la surface n’est pas isotrope, et il y a donc des directions qui pointent naturellement, et vont permettre, faciliter, la croissance dans ces directions.
Ainsi, on peut voir les quatre pointes saillant dans le berlingot, comme des axes privilégiés, non pas « cristal- lographiques », mais des axes de croissance que la surface préfère, bien que l’ordre ne soit pas un ordre atomique. Ainsi, les fibres définissent une anisotropie microscopique (un côté gauche, un côté droit, et une direction privilégiée), qui va se traduire, sur une calotte sphérique, par des directions privilégiées de croissance. La croissance den- dritique d’une empreinte digitale, en quelque sorte, donnerait quelque chose comme un poumon. Sur la gravure, les anneaux de cartilages sont en quelque sorte les empreintes digitales du poumon.
Ces images montrent que tous les branchements et alvéoles du poumon sont en fait définis par les positions des fibres. Le poumon est en quelque sorte une vaste arborescence de fibres, un grand flocon de fibres. On peut dire un peu la même chose des végétaux, dont les fibres, de ce point de vue, nous sont plus familières et évidentes.
En fait, la structure tissée du vivant est tellement proche d’un véritable tissu qu’on peut se demander si l’homme n’a pas simplement emprunté à la nature l’idée du tissage.
Il existe des palmiers, par exemple, dont l’épiderme, en se desséchant, laisse tomber des pans de toile qui ressemblent à s’y méprendre à de la toile de jute. Vous pouvez voir ce genre de toile dans des palmiers en bacs, à la terrasse d’une brasserie ou d’un jardin public. Je suis prêt à parier que beaucoup de passants pensent que c’est un emballage, les restes du sac dans lequel était la jeune pousse avant d’être replantée.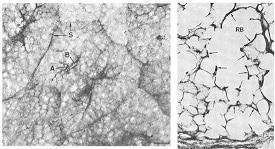
S’agissant des tuyauteries animales ou végétales, il existe d’autres effets. Par exemple : l’alignement dans le sens de l’écoulement tend à régulariser les tuyaux. Cet effet est visible aussi dans l’image du Plat Gousset : les rivières plus grandes tendent à êtres plus lisses sur de plus grandes distances. C’est également vrai des tuyaux vivants. Il existe encore un autre effet, dû à la réaction de la « viande » autour. Qu’on me permette de dire ici, simplement, que les tuyaux, comme les vaisseaux, ne poussent pas dans du vide.
Dans une image comme celle de la vasculature de l’œil de porc, la viande autour des vaisseaux a été dissoute, détruite, pour voir apparaître le moulage de l’intérieur des tuyaux, dans toute leur splendeur. L’inconvénient de ce procédé, c’est qu’il donne à penser que la chair autour des tuyaux ne joue aucun rôle, tout ne semble advenir qu’à l’intérieur des tuyaux, le reste pourrait presque être du vide. Et, de fait, les modèles de morphogenèse existants négligent en général la chair autour des tuyaux.
Cependant, si l’on suppose que les tissus des tuyaux ont un effet sur leur forme, si l’on suppose que les tissus des tuyaux réagissent aux forces mécaniques, si l’on suppose… ne doit-on pas en supposer autant pour la chair entre les interstices ? Si on prend en compte une réaction active des tissus entre les vaisseaux, on obtient des branches régulières ; si le tissu est régulier, comme le sont les distributions de fibres dans les muscles, ou bien les couches de cortex, on trouvera des régularités concomitantes des vaisseaux (de même que les nervures des feuilles simples s’alignent avec les cellules qui forment les « palissades » c’est le nom de la surface des feuilles).
J’ai dit plus haut que j’allais présenter deux mécanismes permettant d’obtenir des choses régulières. J’ai parlé tout d’abord de choses irrégulières qui se régularisent sous l’effet d’un agent matériel. Il s’agissait de formes de croissance, comme celles qu’on rencontre en biologie, surtout. Je vais maintenant évoquer des choses qui sont d’emblée régulières, sous l’effet de ce qu’on appelle une brisure de symétrie. Ce mécanisme a déjà été beaucoup décrit, donc je serai bref. Je fais donc un petit retour sur l’exemple déjà cité de la chipsification. J’ai dit qu’une chips se contracte en prenant la forme d’une selle de cheval. D’une forme circulaire, identique dans toutes les directions, on est passé à une forme qui ondule comme une jupe de mariée : dans certaines directions ça monte, dans d’autres ça descend.
C’est régulier aussi, mais moins qu’un cercle parfait. La selle de cheval a des symétries (gauche/droite, devant/derrière) mais c’est moins symétrique qu’un cercle parfait. On dit donc qu’on passe d’un cercle à la selle de cheval par une brisure de symétrie. Mais en fait, cette brisure de symétrie, simple à comprendre, du moins dans le résultat final, n’est qu’un cas parmi beaucoup d’autres de brisures de symétrie. Ainsi, si l’on cuisait une énorme chips, disons de un mètre, on n’obtiendrait pas une selle de cheval de quatre-vingt-dix centimètres, mais plutôt une succession d’alvéoles et de bosses, un peu comme une boîte d’œufs.
La brisure de symétrie, ici, transforme une grande feuille plate en un réseau régulier de creux et de bosses. La selle de cheval est toujours là, mais reproduite un très grand nombre de fois, aux coins de chaque creux. De même que, suivant la forme et la tension d’une corde de guitare, les ondulations d’une corde sont plus ou moins nombreuses (et le ton différent), de même, suivant l’intensité des forces d’écrasement (de poussée, de tension, etc.), on obtient un nombre déterminé de plis, peut-être plus grand que un. Ainsi, certaines chips ont plus d’un pli en selle de cheval, des fois deux, ce qui les fait ressembler à d’autres grignoteries entortillées (mais cuites sur le même mode que la bonne vieille chips). C’est le cas des Chipsters, de Belin, qui ont souvent une forme en S, plus ondulée qu’une simple chips. Le nombre total de plis effectivement observés peut être arbitraire.
Le fait que ces plis soient très réguliers sera affaire de contexte, une fois encore : si le milieu est très uniforme, s’il n’y a pas de grumeaux, si la poussée est régulière, sans à-coups, la répartition des plis sera aussi propre et régulière que les motifs d’un tissu Vichy. De même, l’orientation des plis sera déterminée par de petits effets, les grumeaux ou les propriétés microscopiques du milieu, comme une légère tendance à s’aligner avec des filaments, avec la direction de la gravité, ou avec toute autre « instruction » résiduelle (comme la lumière de la pleine lune pour certaines algues).